2017年，南方科技大学物理系卢海舟教授课题组和北京大学量子材料中心谢心澄院士合作在《物理评论快报》(Physical Review Letters) 发文预言了三维量子霍尔效应的一种全新的新机制 [1] (南方科技大学新闻链接http://www.sustc.edu.cn/news_events_/4248)。2018年12月18日，英国《自然》(Nature) 杂志在线刊登了复旦大学修发贤课题组的实验进展，验证了这种全新的三维量子霍尔效应 [2]，卢海舟教授为参与作者。最近，卢海舟教授应邀为《国家科学评论》(National Science Review) 特别撰写展望(Perspective), 介绍这种三维量子霍尔效应的新机制 [3]。

            

图1  2016年诺贝尔物理学奖—— “拓扑物态与拓扑相变”

2016年的诺贝尔物理学奖颁发给了拓扑物态和拓扑相变的研究者 (如图1左图所示)。其中1/4的原因是Thouless等人发现了拓扑陈数对“量子霍尔效应”(1985年诺贝尔物理学奖) [4] 的数学描述 [5] (如图1右图所示)。

霍尔效应与量子霍尔效应

我们在高中就学习过霍尔效应。在磁场中，电子感受到垂直于磁场和运动方向的洛伦兹力，发生偏转，并在两端形成电势差，这一现象称为霍尔效应 (如图2左图所示)。因为霍尔效应是磁场引发的，所以横向电压和纵向电流的比值，即霍尔电阻，应该正比于磁场。

但是，1980年von Klitzing发现二维电子气在强磁场作用下，霍尔电阻量子化成一些整数描述的平台，同时纵向电阻消失，这就是量子霍尔效应 (如图2中图所示)。

量子霍尔效应的发现打开了拓扑学这门数学进入凝聚态物理研究的大门。迄今为止，已经有三次诺贝尔物理学奖和量子霍尔效应有关，分别是1985年量子霍尔效应，1998年的分数量子霍尔效应，以及2016年的拓扑物相和拓扑相变。

      

图2  霍尔效应 (左) 与量子霍尔效应 (中)

为什么会有量子化的霍尔效应？

在强磁场下，二维电子气被量子化成离散的朗道能级 (如图3左图所示)。当费米能量处于两个朗道能级之间时，朗道能级在样品边缘形变并切过费米能量，在边缘上产生一维的导电通道，或称为边界态。由于边界态的导电方向已经被磁场限制，没有背散射，因此每个边界态可以无耗散地输运电子，并产生大小为e²/h的电导。这就会导致量子化的霍尔电阻平台和消失的纵向电阻。

量子霍尔效应中无耗散的边界态有望在未来用于实现低能耗高效率的电子器件。

         

图3  为什么会有二维量子霍尔效应(左)以及三维很难量子化(右)

从二维到三维

自从二维量子霍尔效应被发现以来，就开始有理论工作探讨如何在三维体系中实现量子化。在三维体系中，沿着磁场的方向电子感受不到洛伦兹力，动量仍然是好量子数。所以，朗道能级变成沿磁场方向有色散的朗道能带 (如图3右图所示)。无论费米能在哪里，都不可能避免地和体态相切。体态载流子的电子输运并不能实现量子化。因此，在三维体系中通常观察不到量子霍尔效应。如果想观察到量子化，必须要求打开体态能隙，使费米能处于两个朗道能级之间。

早期的理论集中于讨论如何打开体态能隙，比如利用电荷密度波或自旋密度波 [6]、极弱层间耦合等机制 [7]。偶尔会在三维样品中观察到量子霍尔平台 [8-14]，并且符合之前提出的理论图像，包括南方科技大学物理系张立源副教授课题组最新的接收的Nature文章 [15]。以前所有的三维量子霍尔效应都是关于霍尔电导率的量子化。寻找三维量子霍尔效应的新机制并在实验中实现仍然是个有挑战的题目。

        

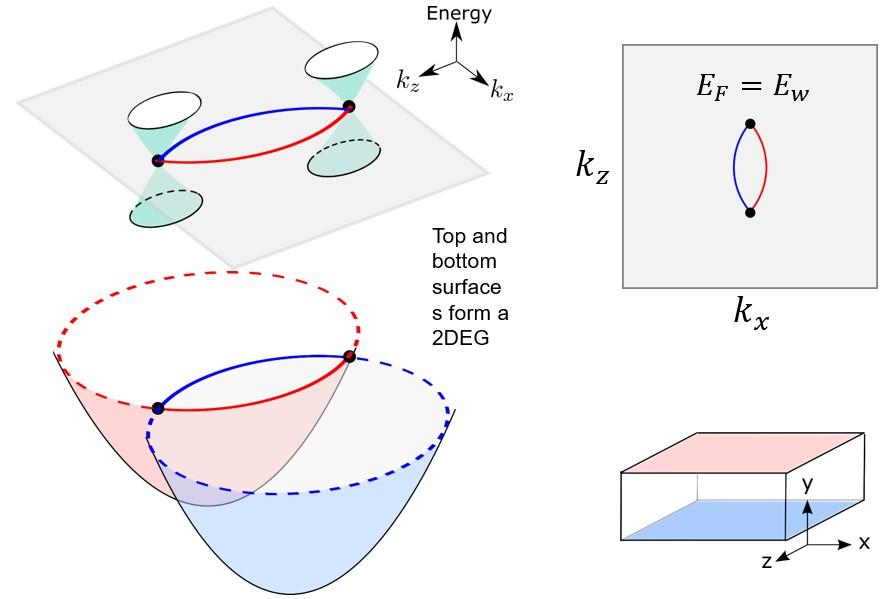
图4  拓扑Weyl半金属的费米弧和Weyl点。每条 (红实线和蓝实线) 费米弧代表半个拓扑保护的二维电子气的费米面，它们分别处于样品的上表面(淡粉)和下表面(淡蓝)，并通过Weyl点 (黑点) 连接构成完整的电子气体系

新的三维量子霍尔效应机制

最近，南方科技大学卢海舟教授和北京大学谢心澄院士的课题组，在拓扑半金属中，利用费米弧和“虫洞隧穿”构成的Weyl轨道，提出了一种新的三维量子霍尔效应机制 [2]。拓扑半金属是拓扑物相的新成员 [16,17]，具有拓扑保护的表面态，被称作费米弧 (如图4所示)。费米弧是拓扑半金属拓扑保护的表面态的费米面。在拓扑Weyl半金属中，有4个面可以有拓扑保护的表面态。由于拓扑约束的原因，每个面的表面态只是半个二维电子气。相对的上下表面的费米弧电子气可以通过Weyl点连接起来，组成一个完整的二维电子气。这是非常奇异的物相。

既然费米弧也是一种二维电子气，它们可不可以有量子霍尔效应呢？要研究这个问题，首先要明白什么是形成量子霍尔效应的关键，那就是电子的回旋运动 (如图3左图所示)。电子回旋运动的量子力学描述等价于谐振子，因此会形成等间距的朗道能级。朗道能级在边界发生能量畸变，才会有边界态提供无耗散的电子输运和量子霍尔化电导，即量子霍尔效应。

        

图5  拓扑半金属的单个表面无法支持回旋运动和量子霍尔效应

我们再来看拓扑半金属的费米弧 (如图6所示)。在拓扑Weyl半金属的单个表面，每个费米弧不能取值所有动量角，这意味着电子在磁场的驱动下通过费米弧运动时在实空间无法完成完整的回旋运动，从而拓扑半金属的单个表面无法支持量子霍尔效应。

        

图6  拓扑Weyl半金属的上下表面的费米弧通过Weyl点“虫洞”隧穿可以支持完整的回旋运动和量子霍尔效应

缺失的半个回旋，“虫洞”隧穿来实现

不过没关系。拓扑Weyl半金属的上下表面的费米弧电子气可以形成一个完整的电子气。电子可以在单个表面的费米弧上完成半个回旋运动，然后通过半金属中的Weyl点，隧穿到另一个表面的费米弧完成另一半回旋运动 (如图6所示)。Weyl点是半金属能谱中导带和价带动量空间接触的点。根据量子力学测不准原理，Weyl点在动量上无限小，意味着在空间上就无穷大，原则上可以联系相距无限远的费米弧。这种隧穿类似“虫洞”效应，即低维度的时空可以通过更高维度的时空奇异点相互连接。两个无限远的二维平面合在一起组成完整的二维电子气，然后支持量子霍尔效应，这是一种全新的三维量子霍尔效应的机制。

          

图7  数值模拟100 nm的拓扑半金属。当费米能放到Weyl点处，出现了霍尔电导的量子化平台 [2]

数值模拟

数值模拟结果也确认了这个新的三维量子霍尔效应机制 [1]。他们计算了100 nm的拓扑半金属模型，这个厚度已经不能被认为是二维系统。当费米能处于Weyl点，数值模拟结果出现了霍尔电导的量子化平台 (如图7所示)。特别是，量子化的是霍尔电导，不是霍尔电导率，和厚度无关。

        

图8  “虫洞”隧穿三维量子霍尔效应的边界态只沿着样品的“棱”传播 [1]

更奇异的是，这种三维量子霍尔效应的边界态具有三维分布，只沿着样品的“棱”传播，上表面在一边，下表面在另一边 (如图8所示)。反转磁场后，边界态的位置也会对换。希望未来可以通过各种电子显微技术探测到这种奇特的边界态分布。

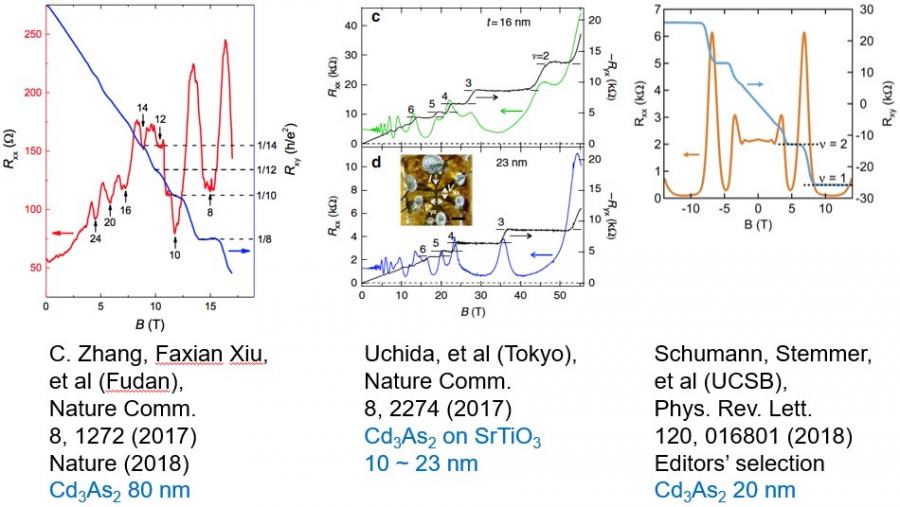
图9  三维量子霍尔效应已经在多个实验中看到迹象，包括复旦大学 [2, 18]、东京大学[19]、加州大学圣巴巴拉分校 [20] 等课题组的报道。

实验进展

目前，已经有多个拓扑半金属实验观察到霍尔电阻的量子化平台 (如图9所示)。这种新奇的三维量子霍尔效应的研究才刚刚开始。直接观测到如图8所示的那种奇异的边界态分布将是未来的一个挑战方向。

参考文献

[1] C. M. Wang, Hai-Peng Sun, Hai-Zhou Lu, and X. C. Xie. 3D quantum Hall effect of Fermi arcs in topological semimetals, Phys.  Rev.  Lett.  119, 136806 (2017).

[2] C. Zhang, et al. Weyl-orbit quantum Hall effect in Cd₃As₂, Nature 565, 331 (2019).

[3] H. Z. Lu. 3D quantum Hall effect, National Science Review doi: 10.1093/nsr/nwy082 (2018).

[4] K. von Klitzing, et al. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance, Phys. Rev. Lett. 45, 494 (1980).

[5] D. J. Thouless, et al. Quantized Hall conductance in a two dimensional periodic potential, Phys. Rev. Lett. 49, 405 (1982).

[6] B. I. Halperin. Possible states for a three-dimensional electron gas in a strong magnetic field, Jpn. J. Appl. Phys. 26, 1913 (1987).

[7] M. Kohmoto, et al. Diophantine equation for the three-dimensional quantum Hall effect, Phys. Rev. B 45, 13488 (1992).

[8] H. L. Stormer, et al. Quantization of the Hall effect in an anisotropic three-dimensional electronic system, Phys. Rev. Lett. 56, 85 (1986).

[9] J. R. Cooper, et al. Quantized Hall effect and a new field-induced phase transition in the organic superconductor (TMTSF)₂PF₆, Phys. Rev. Lett. 63, 1984 (1989).

[10] S. T. Hannahs, et al. Quantum Hall effect in a bulk crystal, Phys. Rev. Lett. 63, 1988 (1989).

[11] S. Hill, et al. Bulk quantum Hall effect in η-Mo₄O₁₁, Phys. Rev. B 58, 10778 (1998).

[12] H. Cao, et al. Quantized Hall effect and Shubnikov-de Haas oscillations in highly doped Bi₂Se₃: Evidence for layered transport of bulk carriers, Phys. Rev. Lett. 108, 216803 (2012).

[13] Y. Liu, et al. Zeeman splitting and dynamical mass generation in Dirac semimetal ZrTe₅, Nature Commun. 7, 12516 (2016).

[14] H. Masuda, et al. Quantum Hall effect in a bulk antiferromagnet EuMnBi₂ with magnetically confined two-dimensional Dirac fermions, Sci. Adv. 2, e1501117 (2016).

[15] F. Tang, et al. Three-dimensional quantum Hall effect and metal-insulator transition in ZrTe₅, arXiv:1807.02678 (2018) Nature in press.

[16] X. Wan, et al. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates, Phys. Rev. B 83, 205101 (2011).

[17] Z. Wang, et al. Three-dimensional Dirac semimetal and quantum transport in Cd₃As₂, Phys. Rev. B 88, 125427 (2013).

[18] C. Zhang, et al. Evolution of Weyl orbit and quantum Hall effect in Dirac semimetal Cd₃As₂, Nature Commun. 8, 1272 (2017).

[19] M. Uchida, et al. Quantum Hall states observed in thin films of Dirac semimetal Cd₃As₂, Nature Commun. 8, 2274 (2017).

[20] T. Schumann, et al. Observation of the quantum Hall effect in confined films of the three-dimensional Dirac semimetal Cd₃As₂, Phys. Rev. Lett. 120, 016801 (2018).