南科大卢海舟团队在三维量子霍尔效应理论取得重要进展
1980年,量子霍尔效应的发现成为了物理学史上最激动人心的篇章之一。量子霍尔效应表现为,在非常低的温度和非常高的磁场下,霍尔电阻量子化为h/e2的整数倍[2] (h是普朗克常数,e是电子电量)。此后,物理学家们还发现了如量子反常霍尔效应等不需要磁场的版本[3]。在量子霍尔效应被发现的这几十年,已经诞生了3个诺贝尔物理学奖,与之相关的拓扑物态也成为物理学的重要研究方向。
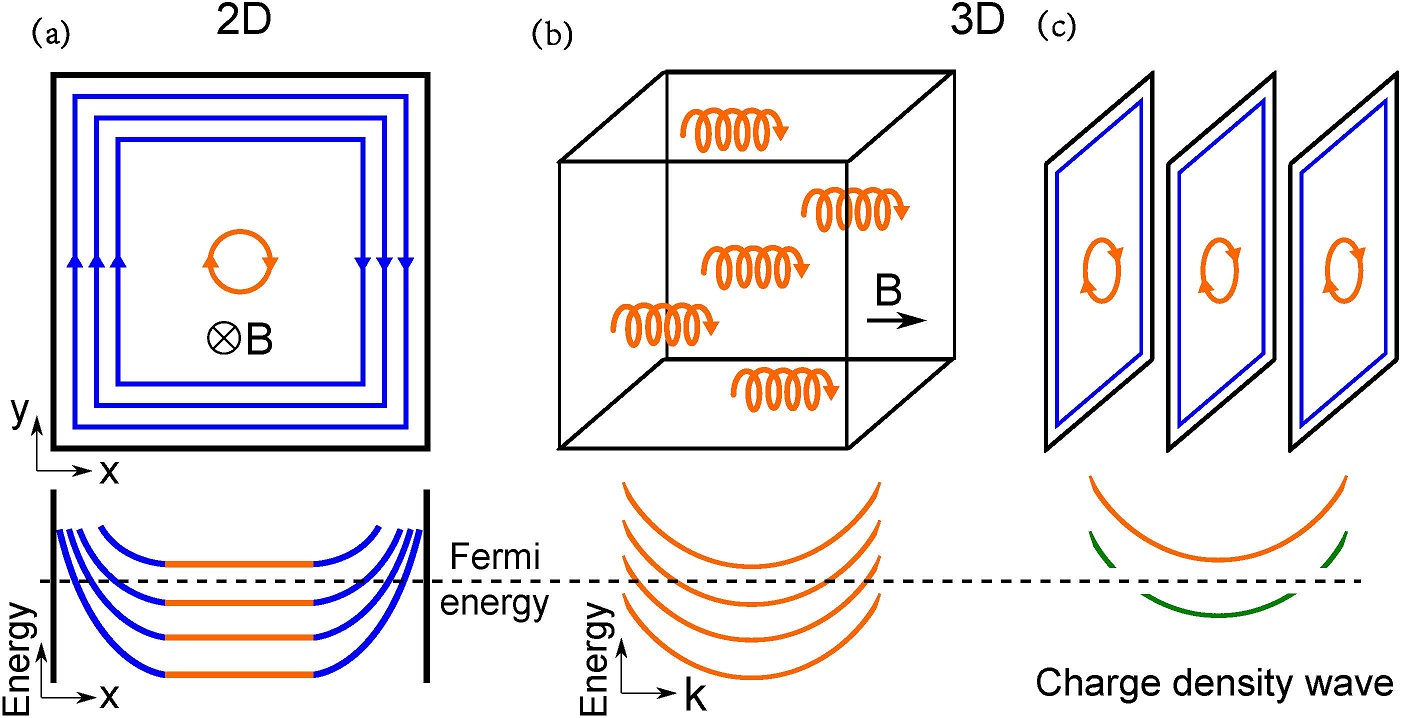
(a)在二维体系中,量子霍尔效应出现时,只有边缘态(蓝色)传导电子,而内部体态是绝缘的,因为费米能量位于朗道能级之间。(b)在三维,朗道能级成为沿着磁场方向色散的一维朗道能带。量子霍尔效应在三维中很难实现,因为费米能量总要穿过一些朗道能带,所以体态是金属的。(c)电荷密度波可以打开朗道能带的间隙,从而使体态绝缘,可以观察到量子霍尔效应。该图引用自文献[1]
早期的研究认为量子霍尔效应很难在三维体系中实现[4-7],物理学家30年来一直在追求量子霍尔效应的三维版本,但一直没有得到令人信服的结果。直到2019年,南科大的张立源团队成功在化合物ZrTe5上观测到三维量子霍尔效应[8]。张立源团队使用高迁移率低电子浓度的高质量样品,冷却到0.6开尔文,在大小为1.7到2.1特斯拉的磁场范围间观察到了量子化的霍尔电阻平台和0纵向电阻率。在这个实验中,电荷密度波被认为是最有可能的机制。电荷密度波是个关联效应,可以把一个三维系统分成多层的二维量子霍尔效应的叠加。
论文链接:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.125.206601
中文报道:
https://newshub.sustech.edu.cn/zh/html/202012/39222.html
英文报道:
https://newshub.sustech.edu.cn/?p=29105
参考文献
[1] F. Qin, S. Li, Z. Z. Du, C. M. Wang, W. Q. Zhang, D. P. Yu, H. Z. Lu, and X. C. Xie, "Theory for the charge-density-wave mechanism of 3D quantum Hall effect", Phys. Rev. Lett. 125, 206601 (2020).
[2] K. von Klitzing, et al., "New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance", Phys. Rev, Lett. 45, 494 (1980).
[3] C. Z. Chang, J. Zhang, X. Feng, J. Shen, Z. Zhang, M. Guo, K. Li, Y. Ou, P. Wei, L. L. Wang, Z. Q. Ji, Y. Feng, S. Ji, X. Chen, J. Jia, X. Dai, Z. Fang, S. C. Zhang, K. He, Y. Wang, L. Lu, X. C. Ma, and Q. K. Xue, "Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator", Science 340, 167 (2013).
[4] J. R. K. Cooper, et al., "Quantized Hall effect and a new field-induced phase transition in the organic superconductor (TMTSF)2(PF)6", Phys. Rev. Lett. 63, 1984 (1989).
[5] S. T. Hannahs, et al., "Quantum Hall effect in a bulk crystal", Phys. Rev. Lett. 63, 1988 (1989).
[6] S. Hill, et al., "Bulk quantum Hall effect in η-Mo4O11", Phys. Rev. B 58, 10778 (1998).
[7] H. Cao, et al., "Quantized Hall effect and Shubnikov-de Haas oscillations in highly doped Bi2Se3: Evidence for layered transport of bulk carriers", Phys. Rev. Lett. 108, 216803 (2012).
[8] F. Tang, Y. Ren, P. Wang, R. Zhong, J. Schneeloch, S. A. Yang, K. Yang, P. A. Lee, G. Gu, Z. Qiao, and L. Zhang, "Three-dimensional quantum Hall effect and metal-insulator transition in ZrTe5", Nature 569, 537 (2019).



