Researchers make advances in geometric and deformation quantization of mathematical physics
In the field of mathematical physics, the mathematical foundation of quantum mechanics is based on the celebrated Dirac-Von Neumann axioms, which consists of Hilbert spaces and the algebra of operators acting on the Hilbert spaces. Since the phase space of a classical mechanical system is described mathematically as a symplectic manifold, the quantization of a symplectic manifold became one of the central topics in the study of symplectic geometry.
Guided by the Dirac-Von Neumann axioms, there are mainly two schemes of symplectic geometry quantizations: geometric quantization and deformation quantization, which focus on the Hilbert space and observable algebra, respectively. An important and unknown question in mathematical physics is to understand how the observable algebra acts on the Hilbert space.
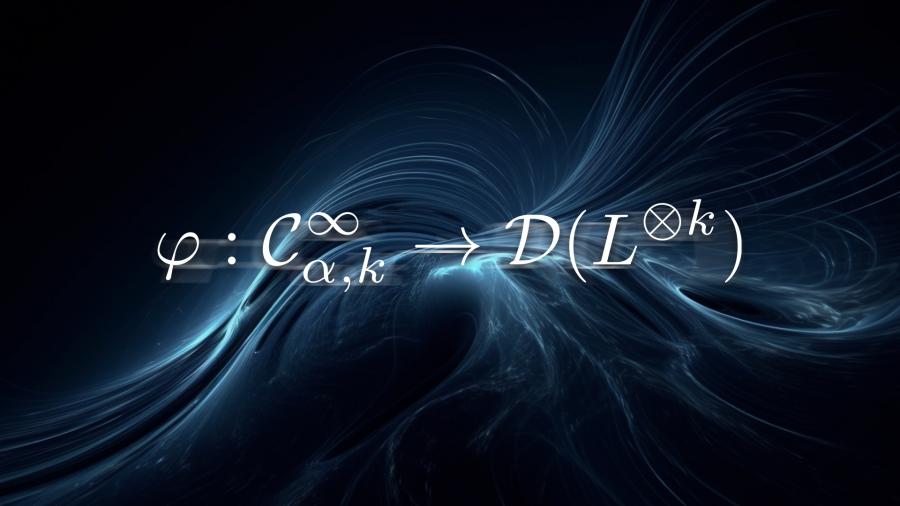
Associate Researcher Qin Li from the Shenzhen Institute for Quantum Science and Engineering (SIQSE) at the Southern University of Science and Technology (SUSTech) has recently made significant progress in geometric and deformation quantization in the field of mathematical physics. This is a joint work with Professors Conan Leung and Kwokwai Chan from the Chinese University of Hong Kong (CUHK). The research team brought up the notion of “non-formal quantization”, and constructed examples of such quantization in Kahler geometry.
Their related results, entitled “Quantizable functions on Kahler manifolds and non-formal quantization”, have been published in Advances in Mathematics, a top journal in mathematics.
To answer the question of how to understand the observable algebra acts on the Hilbert space, the research team conducted a long-term project since 2016. A technical difficulty in answering this question is that the observable algebra (deformation quantization) contains a formal variable h, which corresponds to the Planck constant in physics. The first key step in solving this difficulty is to find a dense sub-algebra in the observable algebra on which the formal variable h can be evaluated.
The researchers focused on Kahler manifolds, equivalently symplectic manifolds with compatible complex polarizations. They used the L infinity structure on these geometric objects and considered its quantum extension, making it a Fedosov abelian connection. These Fedosov connections have surprisingly nice properties, such that they can define a sub-algebra on which the formal variable h can be evaluated. The next step is to extend the Fedosov connection to the study of Hilbert spaces.
Based on these breakthrough observations, the research team gave an explicit action of the sub-algebra on the Hilbert space via the Bargmann-Fock action, which makes this sub-algebra isomorphic to differential operators. These works not only completely solves the open question but also shed some new light on the study of higher dimensional quantum field theories.
Associate Researcher Qin Li from SUSTech and Professor Conan Naichung Leung from CUHK are the joint first authors of this paper. Professor Kwokwai Chan from CUHK is the corresponding author.
This work was supported by the Natural Science Foundation of Guangdong Province, National Natural Science Foundation of China (NSFC), and SUSTech.
Paper link: https://authors.elsevier.com/a/1hl8C_2kE%7ELmK



